
The main topics of the present paper include the ordering of elements in interrogative strings, especially that of the wh-item and the tense morpheme; the modelling of single and multiple wh-fronting and accounting for the variation in the relative ordering of wh-items in terms of optimality-theoretic constraints.
The theoretical framework followed in the paper is Syntax First Alignment (SFA), as developed in Newson (2010) and Newson & Szécsényi (2012). According to SFA, syntax operates on conceptual units (CUs) which are either roots or functional CUs; they are ordered relative to one another and relative to domains, which are formed by CUs. The model assumes a late insertion concept: actual words are inserted only after syntactic ordering of the CUs. Constraints either define precedence/subsequence or adjacency to a CU or to a whole domain. Apart from these, faithfulness requirements are also employed to counterbalance the deletion of indexes which mark CUs as members of a domain.
On the one hand, the difference between single vs. multiple wh-fronting languages has to be reflected in the analysis; on the other hand, multiple wh-questions are possible in single-fronting languages as well, and it is not entirely straightforward which of the wh-items precedes the string. These issues have been explained by the Cluster Hypothesis in the Minimalist framework (Sabel 2001, Nagy 2006). I will argue that referential properties of wh-items, argument ordering and discourse function play a role in determining the primacy of one wh-item over others in a structure.
The paper has the following structure. First, the basic word orders of English, German and Hungarian will be sketched as a point of departure. The analysis of wh-interrogatives begins with single questions discussing the appropriate form of the constraints and the emergence of inversion in matrix clauses. Then I turn to interrogative strings containing more than one wh-element and propose constraints that derive the relative ordering of multiple wh-items correctly.
As Newson (2010, this volume) extensively discusses the ordering of arguments, that of the elements of the verbal complex and the positioning of the finite verb relative to the members of a clause, here I will only briefly list the language-particular rankings, while tableaux will be presented when we reach the analysis of interrogative structures.
Throughout the paper, the types of alignment constraints in (1)–(4) will be employed. Apart from precedence and subsequence, the notion of adjacency should also be mentioned as a basic relation in SFA.
The relevant CUs referring to verbal and temporal elements, as have been worked out for English in Newson (2010), are [tense], [perfect], [passive], and [progressive]. It can be stipulated that the tense is the first element among the verbal features. The ordering in (5) is captured by the constraint set in (6), which contains an ordered set of precedence constraints relative to the temporal domain. The constraints function as follows: if one or more of the verbal features are not present, the corresponding constraints become irrelevant, and the decision is passed over to the lower ranked ones.
| has | been | being | done |
| [tense] | [perfect] | [progressive] | Root[passive] |
The position of the root among the temporal CU is defined as being second to last. This constellation can be achieved by the combination of an anti-alignment and a domain-precedence constraint. Thus, regardless of the other members of the temporal domain, the root will always take second-to-last position and get associated with the functional CU on its right in the output.
A second question concerns the position of the temporal domain as a whole: in matrix declaratives, it follows the subject and other arguments follow it, as the structure in (8).
Thus, it would seem to be reasonable to define the position of the predicate as second in the argument domain, which can be achieved by the following pair of constraints (9). This ordering produces a second-position phenomenon; the temporal domain cannot precede all the arguments but aims to precede the most of them.
The ordering of the arguments, as already discussed, is then possible to define independently of the temporal domain, as in (10). The argument domain is defined as the set of all arguments present in a given input.
However, if we bear in mind that topics may also appear at the front of the argument domain, the situation is not so straightforward any more. For instance, we face a problem in case of a non-subject argument topic, highlighted in boldface in (11), with question marks indicating the possible positions of the temporal domain. The fronted topic is also part of the argument domain, as it bears an argument feature. The above two constraints would place the predicate immediately after the topic in such cases, which is obviously not the right word order in English (but would do well for German).
| [topic][arg₂] | ? | [arg₁] ? | [arg₃] |
| topic | subject | non-subject argument |
The generalization that would capture this situation and an unmarked declarative sentence as well, must be formulated in terms of the first argument: what is true for both cases is that the first argument precedes the temporal domain.
This constraint, in combination with a lower ranked DtemppDarg can account for the second-after-subject position of the finite verbal complex in English declaratives. This way, its more general counterpart, Dtemp*pDarg, becomes unnecessary, thus it will not be represented in tableaux.
Although two different word orders have to be accounted for in German, following standard assumptions, I will take the verb-last word order found in subordinate clauses to be the underlying or unmarked one which reflects the ordering of the verbal-functional features, the matrix verb-second being the result of further constraints on matrix and non-neutral clauses (like questions, topic or focus structures). The most complex temporal domain is presented below, where the ordering of temporal CUs can be best observed. Differently from English, the progressive aspect is not expressed through verbal inflection in German.
| gemacht | worden | ist |
| prtc-make-prtc | become-prtc | is |
| Root[passive] | [perfect] | [tense] |
In the following step, I present the group of constraints that define the relative order of verbal features among themselves (14).
The next issue is to discuss the position of the whole temporal domain: in an embedded environment, the verbal complex is the final element in the string, as shown schematically in (15). It does not only follow arguments but also adjuncts and all other possible material belonging to the input of the string. Thus, the position of the verbal domain has to be defined as in (16), in relation to the predicate domain, which contains all the CUs that are associated with a given predicate in the input.
In present and past tense, the ordering of the tense feature and the verbal root is apparent, as the bound tense morpheme attaches to the right side of the root. In unmarked cases, the preverbal prefix is located to the left of the root (17); it is treated here as a feature of perfectivity as in É. Kiss (2002), but not part of the temporal domain. In inversion structures, the tensed verb switches sides with the verbal prefix, as in (18).
| Jánostop | el- | ment |
| John | away | go-pst |
| [topic] | prefix | Root[tense] |
| PÉTER | ment | el |
| PETER | go-pst | away |
| [focus] | Root[tense] | prefix |
Constraints (19)–(22) reflect the above observations. The root-tense ordering is achieved by (19). To ranking of the adjacency constraints is of importance: in cases when both the root and the prefix precede the tense morpheme, the root has to stay closer to it. The adjacency requirement of the prefix is also fulfilled, when it follows the finite verb.
It has to be noted that the adjacency requirement concerning the verbal root and the temporal domain is not an ad hoc constraint but is supposed to be present in the ranking of other languages as well. As I do not intend to go into unnecessary details regarding the temporal domain in this paper, I will mention it only in connection with Hungarian.
When relating the arguments and the predicate, it can be observed that in clauses without discourse-marked elements, the verb precedes all arguments in the default case.
Moreover, the argument domain in Hungarian does not seem to be ordered: the postverbal order of arguments is free; therefore, I will assume that the argument alignment constraints are ranked on an equal level.
After having laid down the basics of the analysis, let us turn to interrogative structure containing one [wh] feature. Two substantial issues arise in connection with wh-structures which will be considered in the analysis. The first one concerns the proper form of the constraints in order to be able to derive both single and multiple wh-fronting languages. In former optimality theoretic literature, the account of Ackema and Neeleman has a similar aim. They propose the constraints in (26) and (27): Q-Scope is responsible for multiple wh-fronting, as the criterion is defined from the point of view of the wh-item, whereas the other constraint, Q-Marking, is formulated from the perspective of the clause, from which results that it can be fulfilled by a single wh-item as well (1998: 16–17).
The same effect could also be achieved by alignment constraints. The most straightforward idea would be to posit a wh-precedence constraint of the form demonstrated in (28).
This formulation corresponds to the idea of Q-Scope, because it would front all nominal domains containing the wh-feature, as the constraint is one concentrating on the feature itself; thus it will assess every wh-feature with respect to its position. This form of the constraint is presumably operative in languages with multiple wh-movement, like Hungarian.
Another option is to look at the situation from the perspective of the predicate domain: in case of an interrogative predicate, its domain has to be preceded by a [wh] feature, or in other words, it has to follow a [wh] feature. Here, the constraint focuses on the position of the predicate domain, which means that the requirement is satisfied if the domain is preceded by one relevant feature, regardless of the fact how many such features are present in the string.
The second question concerns the position of the finite tense in matrix interrogatives. In all of the languages in question the wh-phrase is directly adjacent to a verbal element in a matrix clause, either to the lexical verb or to an auxiliary. Although inversion is not restricted to interrogative structures, this phenomenon deserves our attention, too. I propose the existence of a constraint which forces the finite tense CU in a matrix clause to be dislocated from the temporal domain and appear in second position.
This lends itself to the question whether it is justified to differentiate between the tense feature in matrix and embedded structures: in my view, it needs to be included in the input, as the nature of the tense morpheme has an effect on vocabulary insertion. If one thinks about the sequence of tenses, it becomes clear that the form of an embedded tense feature is not only determined by its own form but also by the tense in the corresponding matrix clause. Thus, the vocabulary also makes a distinction between “dependent” and “independent” tense features; therefore they must receive some kind of marking in the input.
The matrix tense constraints are assumed to be ordered as in (30), which, again, derives a second-position phenomenon. The matrix [tense] feature must be as close to the front of the predicate domain as possible, but it cannot precede it. This way, the matrix [tense] CU loses its adjacency to the rest of the temporal domain in the majority of cases.
On the basis of the above, it can be stipulated that the tense feature sometimes loses its marker which connects it to the temporal domain, as it appears to be behaving differently from the other domain members. If the system enables the deletion of indexes, it should also be constrained to avoid its excessive application. The general form of the relevant faithfulness constraint is given in (31), while the specific formulation concerning the temporal domain is as (32).
In the following, it will be briefly reviewed whether one of the wh-constraints and the three constraints on verb-second can derive the desired structures in the languages under discussion, i.e., (i) uniform verb-second in German; (ii) inversion in matrix wh-clauses with the exception of subject questions in English; (iii) side-switching of the tensed verb and the verbal prefix in Hungarian interrogatives.
The effects of the tense alignment and faithfulness constraints can be observed in tableau 1, containing a German matrix interrogative. In candidate (a), the tense feature is dislocated from the temporal domain and its index becomes deleted. This way the rest of the temporal domain still follows the argument domain, thus DtempfDpred is satisfied. Candidate (b) with no deleted domain marker, which has the same ordering of CUs as candidate (a), loses on DtempfDpred, as does candidate (c), in which the temporal domain sticks together. Candidate (d) illustrates the embedded word order, ruled out by the constraint tensempDpred demanding the higher position of [tensematrix]. The root has been associated with the high tense instead of the rest of the temporal domain in candidate (e): this violates the root-domain adjacency. The last candidate, (f), demonstrates the effect of the wh-precedence constraint.

A special case should also be mentioned, namely the position of the finite tense and the root in simple tenses, when the temporal domain consist of the tense feature only, as in (33). In such cases, the root does not remain in clause-final position but gets associated with the matrix tense and they are spelt out as one vocabulary item. To rule out the separated tense morpheme and the root in matrix clauses, no extra constraint needs to be introduced: the adjacency requirement between the members of the temporal domain and the verbal root is sufficient to handle this situation. In such cases, no index deletion is necessary, as the temporal domain consists of only one member, the matrix tense CU.
In English, two different patterns emerge in matrix interrogatives. Non-subject questions involve inversion, i.e., the [tense] CU becomes dislocated from the temporal domain and is place between the wh-item and the first argument. As is well known, we find a different pattern in subject questions, where the tense feature stays together with the temporal domain following the subject.
To derive the former structure, the evaluation of an adjunct matrix wh-question is presented in tableau 2. Only candidates (a) and (b) with a [wh] feature in the initial position satisfy the wh-constraint. Candidate (b) fares worse on tensempwh, as one more item, apart from the [wh] CU, precedes it. The [tense] CU is not part of the temporal domain in (a) and (c), thus its index is deleted in these instances.

It has to be demonstrated that the system can also account for the lack of inversion in English subject interrogatives. The difference between the winning candidate (a) and clause (b) lies in faithfulness. In (b), the domain index of [tense] has been deleted, similarly to inversion structures; however, this operation proves to be unnecessary here because the members of the temporal domain are adjacent to one another. Candidates (c) and (d) containing a detached tense morpheme fail either on faithfulness, (c), or because one more argument precedes the temporal CUs, (d), thus violating DtemppDarg to a greater extent than the winning candidate.

In Hungarian, a multiple wh-fronting language, the functioning of the other type of wh-constraint will be assumed, i.e., whpDpred, that refers to every [wh] CU in a string. In addition, one of the fronted wh-items, or the only one in single questions, is immediately preverbal. This position differs from the preverbal position of the topic, as the examples (34) and (35) below demonstrate. The wh-item aims to be closer to the verbal stem bearing the tense feature, forcing the preverbal prefix to appear in postverbal position.
| Az ajándék-ottopic | oda-ad-ta | Zoli | a gyerek-ek-nek. |
| the present-acc | pvp-give-pst | Zoli | the child-pl-dat |
| Mi-twh-item | ad-ott oda | Zoli | a gyerek-ek-nek? |
| what-acc | give-pst pvp | Zoli | the child-pl-dat |
Tableau 4 assesses a single argument wh-question in Hungarian with a prefix verb. As the argument ordering constraints do not play a role in the evaluation, they are left out from the tableau — concerning argument order, only the DtemppDarg requirement is regarded as important, as it places the predicate before the arguments in the default case and is able to measure deviations from the basic structure. The tense-precedence constraint rules out both candidate (b), in which the prefix is preverbal and candidate (d) with a preverbal subject in addition to the preverbal wh-item. Candidate (c) with verb-initial word order loses on

As already discussed, the language-specific property whether all or only one wh-phrase fronts the clause can be derived by the dominance of a feature-domain or a domain-feature precedence constraint. In tableau 5 the working of the wh-precedence constraint can be witnessed through the evaluation of a Hungarian multiple question. The requirement that all [wh] features should come in front of the predicate domain is best fulfilled by candidates (a) and (c), in which the two features precede all other items. Nevertheless, [wh]pDpred can never be fully satisfied if the string contains two or more [wh] CUs, as all of them count as part of the argument domain, i.e., if one wh-item precedes the other, it counts as a violation. In spite of that, multiple fronting is still assessed as the best option, as in other cases (candidates (b), (d), (e)) the interrogative CUs are located further away from the initial position, which can be measured by the wh-precedence constraint due to its gradient nature.

Having achieved this, the next topic concerns the internal makeup of multiple questions, more precisely, which factors have an effect on the ordering of multiple wh-items in a fronted cluster, and on what grounds it is decided which of them is fronted in a single-movement type language.☞The description of the data relies on Rudin’s (1988) exhaustive study on multiple wh-movement.
Interestingly, the ordering principles regarding multiple wh-items can be similar in languages with single and multiple fronting strategies, i.e., the cross-linguistic differences regarding these principles do not coincide with the single vs. multiple movement line of division.
We find a clear cross-linguistic distinction across languages regarding the subject wh-item. In languages like English and Bulgarian (a multiple wh-fronting language), no other expression containing a wh-feature can precede the first argument if it is also associated with a wh-feature.☞These and the following Bulgarian examples are taken from Bošković (1999).
| a. | Koj | kogo | vidja? |
| who | whom | saw | |
| b. | Kogo | koj | vidja? |
| whom | who | saw |
| Koj | kakvo | na kogo | e | dal? |
| who | what | to whom | has | given |
Such strict ordering is easily captured by the combination of one of the wh-precedence constraints and the ones concerning the order of the arguments and the temporal domain.
In spite of the strict superiority of wh-subjects in English, other wh-items seem to be freer in their relative ordering, as the following examples demonstrate.
It goes without saying that in languages without superiority effects, we also find similar variation, including wh-subjects, as in the German examples in (41) and the Hungarian ones in (42).
| a. | Wen | hat | wer | gesehen? |
| who-acc | has | who-nom | prtc-see-prtc | |
| b. | Wer | hat | wen | gesehen? |
| who-nom | has | who-acc | prtc-see-prtc |
| a. | Mi-t | mikor | csinálsz? | |
| what-acc | when | do-2sg | ||
| b. | Mikor | mi-t | csinálsz? | |
| when | what-acc | do-2sg | ||
| c. | Hova | ki | mikor | utazott? |
| where | who | when | travel-pst-3sg |
This state of affairs needs further investigation as well, as optionality is not frequent in language; thus, the word order variants cannot be regarded as equal in meaning. Moreover, the present constraint set developed for the description of basic word order would render the variant as optimal which stands closest to the basic argument order, other orders would count as suboptimal.
This is demonstrated by tableau 7 containing a multiple interrogative, in which both of the wh-items function as arguments, represented as [wh]arg₂ and [wh]arg₃. On the basis of its grammaticality, candidate (e) should be assessed optimal, as well, but loses on the argument ordering constraints, as a lower argument is fronted than in sentence (a).
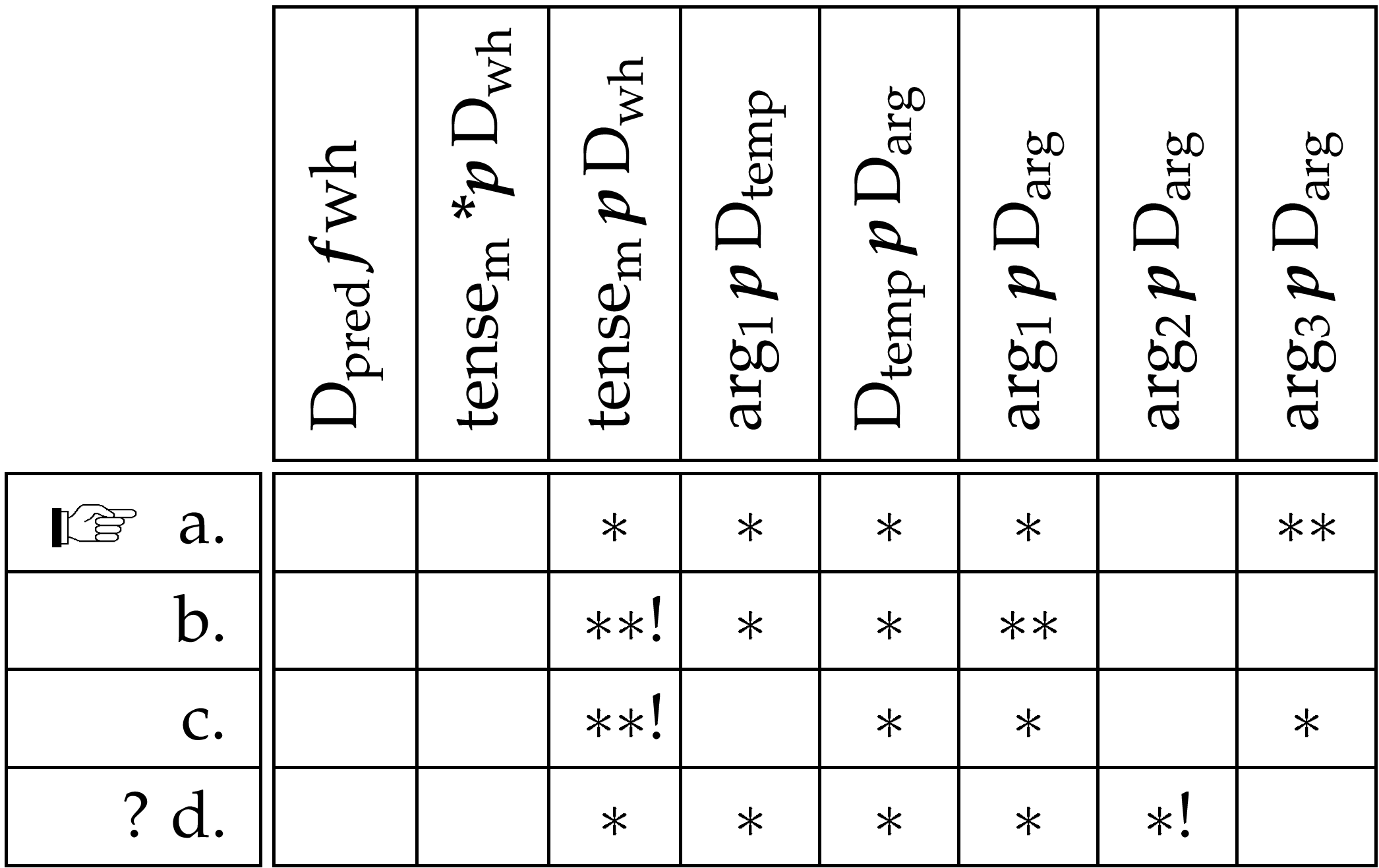
Newson (this volume) suggests that a fronted wh-item looses its argument domain membership, i.e., technically speaking, its domain marker or index will be deleted. This way, it does not violate the argument ordering constraints but still belongs to the clause, i.e., to the predicate domain. Although this view seems promising, we face considerable difficulties, as tableau 8 demonstrates. The relevant faithfulness constraint concerning the indexes of the argument domain is abbreviated as

Another possible solution to this problem would be to consider on what other basis nominal items are ordered. It can be hypothesized that the fronted wh-item, and the first wh-item in multiple-fronting languages like Hungarian, has a topical character and therefore bears the weak topic feature, i.e., [about].
Imrényi discusses the structure of multiple interrogatives in Hungarian from a cognitive perspective, and calls the first of two wh-items in a Hungarian clause “topikkérő” (2012: 156), i.e., “topic requesting expression”, based on answer patterns of multiple questions. It is claimed that the structure of a question anticipates the structure of the answer,☞A “kérdések szerkezete gyakran megelőlegezi a válaszmondat szerkezetét” (Imrényi 2012: 156). in the case of multiple questions, the answer to the first wh-item functions as the topic of the clause, whereas the answer to second one functions as focus. These observations are translated in term of alignment in (43). The coindexation on the CUs indicates that the relevant features have to be in the same nominal expression, i.e., they are not adjacent by chance.
In English, the constraint should be located under arg₁pDarg as in tableau 9, to ensure that a wh-subject is not affected by it, i.e., will always be the fronted one in multiple structures. Out of the two grammatically correct candidates from the previous tableau, the constraint chooses the one in which the about-marked interrogative item is fronted.
| Candidates: | (a), (c) What has Jon been saying to whom? |
| (b), (d) To whom has Jon been saying what? |

In German, differently from English, [whi][abouti]p[wh] overrides all the argument ordering constraints. This way it can account for the wh-object > wh-subject order in example (41a) above. The hierarchy with the constraints regulating wh- and argument order is presented in (44).
Although the above problem does not arise in Hungarian, as it has been assumed that the argument constraints are equally ordered, the insertion of the wh-topic constraint helps to reflect interpretational differences, i.e., that different orderings correspond to inputs with distinct discourse-functional interpretation. This is illustrated by tableau 10 containing two syntactically correct alternatives, in which the [whi][abouti]p[wh] constraint prefers the precedence of the proto-topical wh-item in candidate (a).

In the above treatment of multiple questions, both argument and adjunct wh-items has been mentioned. However, there is a type of adjunct which seems to behave differently from other clause members, i.e., non-referential wh-adjuncts like how and why. Languages fall into two categories according to the behaviour of non-referential wh-adjuncts: (i) in languages like English, (45), such a wh-item has to precede the other(s) regardless of their argument status; (ii) in the other group exactly the reverse situation holds, i.e., a non-referential wh-item can never be the first among other wh-items. The latter state of affairs is demonstrated by examples from Bulgarian, in (46), German, in (47) and Hungarian, in (48).
| a. | Koj | kak | udari | Ivan? |
| who | how | hit | Ivan | |
| b. | *Kak | koj | udari | Ivan? |
| how | who | hit | Ivan |
| Wen | hat | Maria | warum | ge-küss-t? |
| who-acc | has | Mary | why | prtc-kiss-prtc |
| a. | Ki | miért | rajzol-t | macská-t? |
| who | why | draw-pst | cat-acc | |
| b. | *Miért | ki | rajzol-t | macská-t? |
| why | who | draw-pst | cat-acc |
Here again, I opt for privative instead of binary features, as they can model the complexity of structures more adequately: if a CU, carrying e.g. pragmatic or morphological information, is present, the expression is “bigger” than in the absence of it. A similar effect cannot be achieved by using binary features of the form [±ref]. The [ref] feature stands for the referentiality of a nominal expression; its absence means non-referentiality. Both the precedence and subsequence versions of the constraint have visible effects, it depends on the language type which of them is observed, i.e., ranked higher.
These constraints must be fairly dominant in the constraint hierarchy in the languages under discussion, especially in English-type languages, as the referentiality constraint is assessed more important than the observation of argument order. The ranking in (51) derives languages like Bulgarian, German and Hungarian, in which non-referential wh-words cannot precede referential ones; the reverse ranking accounts for the English facts, for instance.
One of the aims of the paper has been to provide further support for the applicability of a structureless theory of grammar. With the use of alignment and faithfulness constraints a wide range of phenomena connected to interrogative structures can be accounted for, including verb positions, number and additional features of fronted wh-items. It has been demonstrated that a simple set of alignment constraints can be applied to model several dimensions of cross-linguistic variation. In sum, it can be stated that the present optimality theoretic framework yields promising results in deriving word order regularities.
Ackema, Peter and Ad Neeleman. 1998. WHOT? In: Pilar Barbosa, Danny Fox, Paul Hagstrom, Martha McGinnis, and David Pesetsky (eds.), Is the Best Good Enough? Optimality and Competition in Syntax. Cambridge, MA: The MIT Press. 15–35.
Bošković, Željko. 1999. On multiple feature checking. In: David Samuel Epstein and Norbert Hornstein (eds.), Working Minimalism. Cambridge, MA: The MIT Press. 161–188.
É. Kiss, Katalin. 2002. The syntax of Hungarian. Cambridge: Cambridge University Press.
Imrényi, András. 2012. A magyar mondat viszonyhálózati modellje. PhD dissertation. Eötvös Loránd University, Budapest.
Nagy, Gizella Mária. 2006. Multiple questions in English, German and Hungarian. A cluster-based approach. The Even Yearbook 7. (seas3.elte.hu/delg/publications/even/2006.html#na)
Newson, Mark. 2010. Syntax first, words after: a possible consequence of doing Alignment Syntax without a lexicon. The Even Yearbook 9. (seas3.elte.hu/delg/publications/even/2010.html#ne)
Newson, Mark and Krisztina Szécsényi. 2012. Dummy Auxiliaries and Late Lexical Insertion. The Even Yearbook 10: 80–125. (seas3.elte.hu/delg/publications/even/2012.html#ns)
Rudin, Catherine. 1988. On multiple questions and multiple wh-fronting. Natural Language and Linguistic Theory 6: 445–501.
Sabel, Joachim. 2001. Deriving multiple head and phrasal movement: The Cluster Hypothesis. Linguistic Inquiry 23: 532–545.